Synthetic control with pymc models

import arviz as az

import causalpy as cp

%load_ext autoreload
%autoreload 2
%config InlineBackend.figure_format = 'retina'
seed = 42

The autoreload extension is already loaded. To reload it, use:
  %reload_ext autoreload

Load data

df = cp.load_data("sc")
treatment_time = 70

Run the analysis

Note

The random_seed keyword argument for the PyMC sampler is not neccessary. We use it here so that the results are reproducible.

# Note, we do not want an intercept in this model
result = cp.pymc_experiments.SyntheticControl(
    df,
    treatment_time,
    formula="actual ~ 0 + a + b + c + d + e + f + g",
    model=cp.pymc_models.WeightedSumFitter(
        sample_kwargs={"target_accept": 0.95, "random_seed": seed}
    ),
)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [beta, sigma]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 12 seconds.
Sampling: [beta, sigma, y_hat]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]

fig, ax = result.plot(plot_predictors=True)

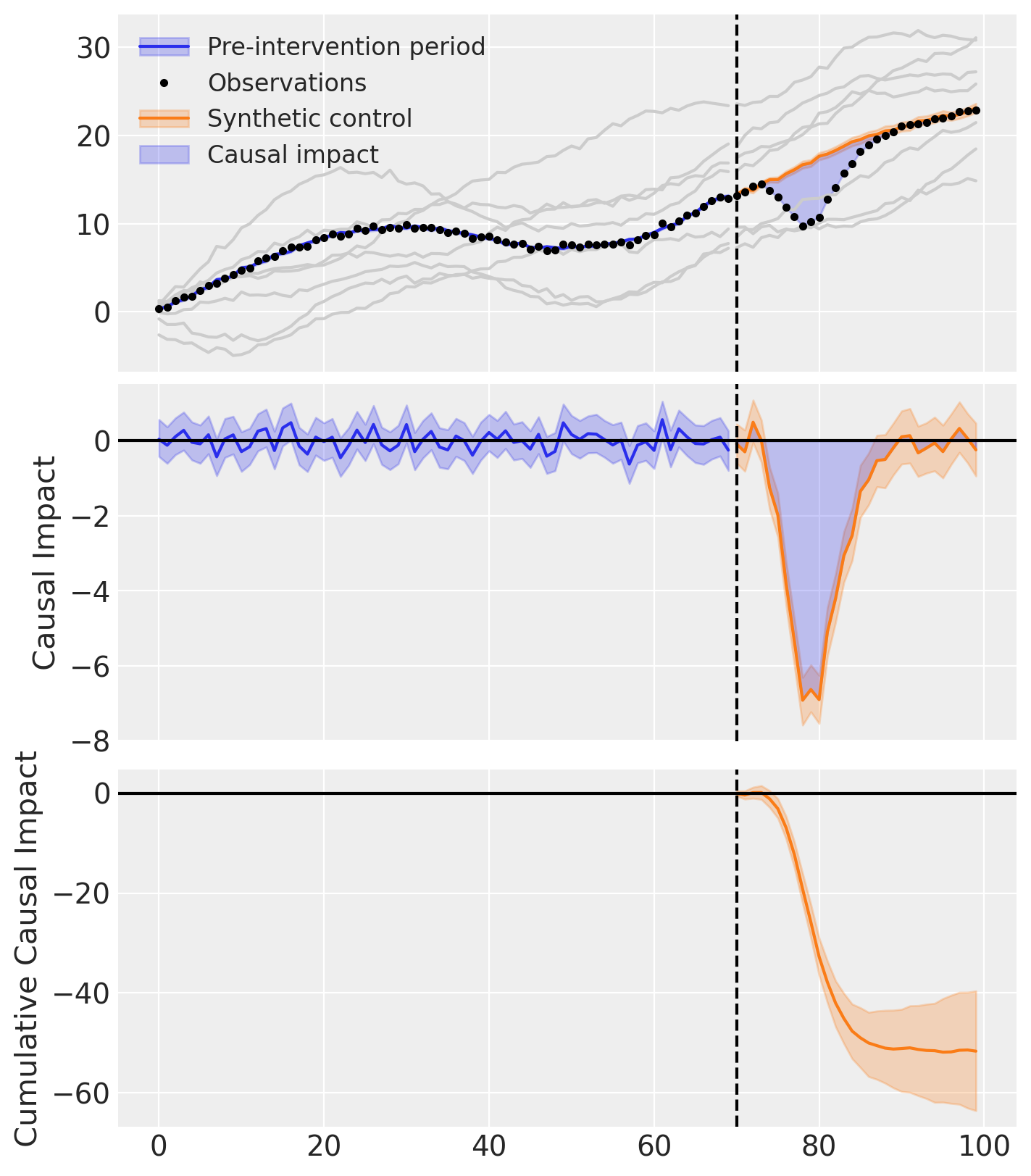
result.summary()

==================================Pre-Post Fit==================================
Formula: actual ~ 0 + a + b + c + d + e + f + g
Pre-intervention Bayesian $R^2$: 0.98 (std = 0.0029)
Model coefficients:
    a      0.34, 94% HDI [0.3, 0.38]
    b      0.049, 94% HDI [0.01, 0.089]
    c      0.3, 94% HDI [0.26, 0.35]
    d      0.054, 94% HDI [0.01, 0.099]
    e      0.024, 94% HDI [0.0012, 0.066]
    f      0.19, 94% HDI [0.11, 0.26]
    g      0.039, 94% HDI [0.0029, 0.088]
    sigma  0.26, 94% HDI [0.22, 0.31]

As well as the model coefficients, we might be interested in the avarage causal impact and average cumulative causal impact.

az.summary(result.post_impact.mean("obs_ind"))

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
x	-1.721	0.218	-2.118	-1.32	0.006	0.004	1240.0	1821.0	1.0

Warning

Care must be taken with the mean impact statistic. It only makes sense to use this statistic if it looks like the intervention had a lasting (and roughly constant) effect on the outcome variable. If the effect is transient, then clearly there will be a lot of post-intervention period where the impact of the intervention has ‘worn off’. If so, then it will be hard to interpret the mean impacts real meaning.

We can also ask for the summary statistics of the cumulative causal impact.

# get index of the final time point
index = result.post_impact_cumulative.obs_ind.max()
# grab the posterior distribution of the cumulative impact at this final time point
last_cumulative_estimate = result.post_impact_cumulative.sel({"obs_ind": index})
# get summary stats
az.summary(last_cumulative_estimate)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
x	-51.635	6.537	-63.546	-39.591	0.185	0.131	1240.0	1821.0	1.0

Validating the model fit

If we want, we can also conduct our parameter estimation on a portion of the pre-intervention period data, but leave a short validation period before the intervention. This allows us to see how well the model fits the data and could be a good idea if we have concerns about overfitting, or poor ability of the model to produce accurate forecasts thus a poor counterfactual prediction.

The intervention period was 70, so we could choose whatever we think is appropriate as the validation time. Here we choose 50, so that we have 20 observations which are not used in the parameter estimation that we can use to evaluate the ability of the model to forecast the outcome.

validation_time = 50

result = cp.pymc_experiments.SyntheticControl(
    df,
    treatment_time,
    validation_time=validation_time,
    formula="actual ~ 0 + a + b + c + d + e + f + g",
    model=cp.pymc_models.WeightedSumFitter(
        sample_kwargs={"target_accept": 0.95, "random_seed": seed}
    ),
)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [beta, sigma]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 14 seconds.
Sampling: [beta, sigma, y_hat]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]

result.plot();

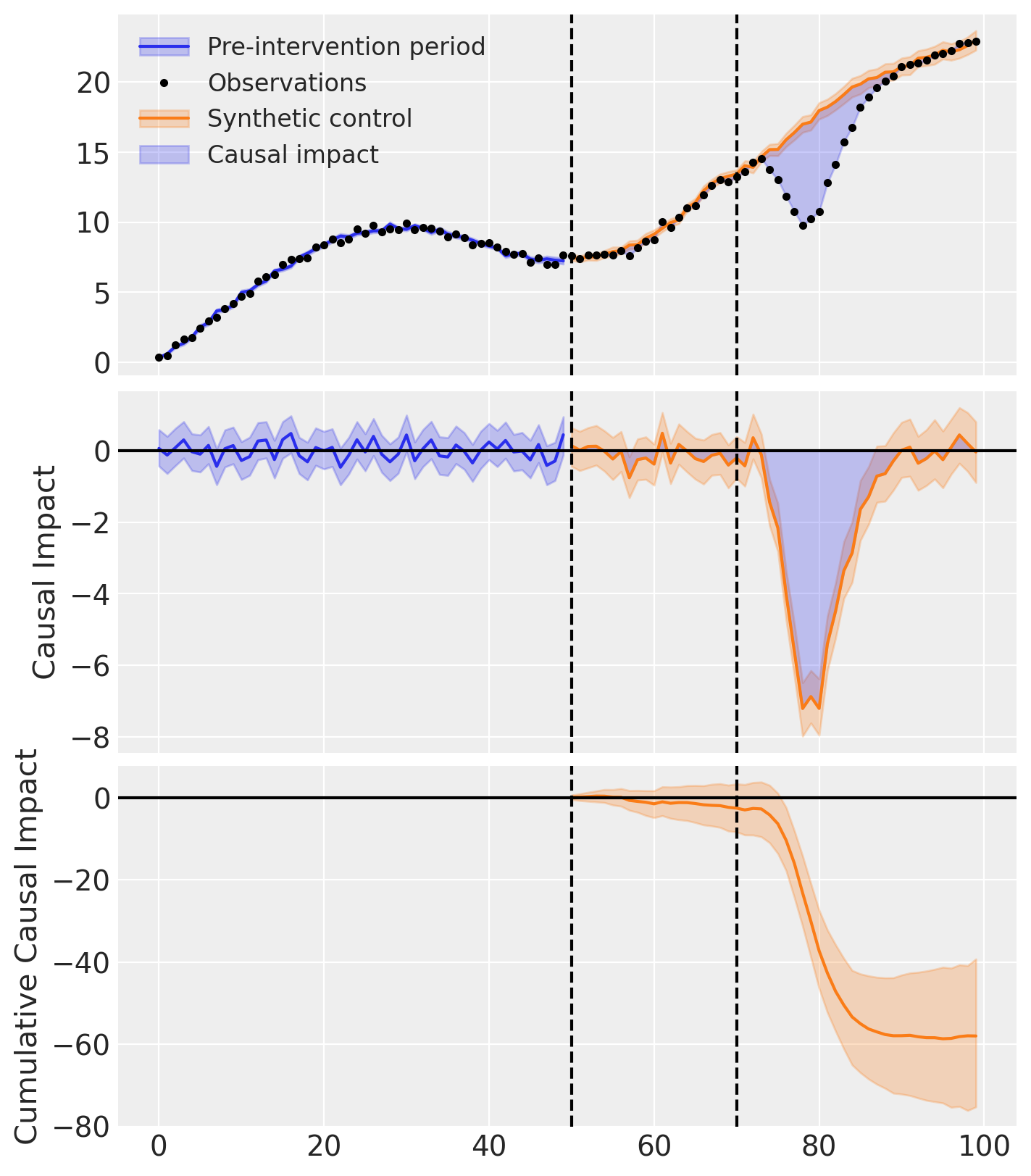
result.summary()

==================================Pre-Post Fit==================================
Formula: actual ~ 0 + a + b + c + d + e + f + g
Pre-intervention Bayesian $R^2$: 0.98 (std = 0.0038)
Validation Bayesian $R^2$: 0.97 (std = 0.0098)
Model coefficients:
    a      0.36, 94% HDI [0.31, 0.41]
    b      0.06, 94% HDI [0.0093, 0.11]
    c      0.31, 94% HDI [0.25, 0.37]
    d      0.037, 94% HDI [0.0018, 0.091]
    e      0.057, 94% HDI [0.0048, 0.12]
    f      0.12, 94% HDI [0.012, 0.23]
    g      0.053, 94% HDI [0.0045, 0.11]
    sigma  0.26, 94% HDI [0.22, 0.32]